Installation
The easiest way to insatll CUDA is to use the standard installation form a package
sudo apt install nvidia-cuda-toolkit sudo apt-get install libglu1-mesa libxi-dev libxmu-dev libglu1-mesa-dev
On Ubuntu 18.04 it will install the Cuda version 9.
Vocabulary
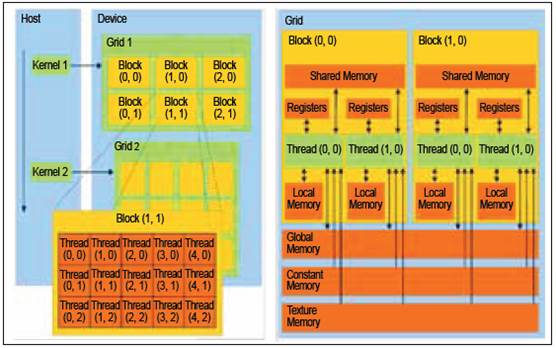
A small definition of concept is necessary to understand the CUDA architecture.
Host An another word to say the CPU of the running machine.
Device: The GPU itself
Kernel Function or portion of code that runs on a grid
GridSet of blocks
BlocksSet of threads
ThreadsSmallest unit of execution
Ouch.
Surprisingly the smallest unit of a GPU is called a thread (so a different meaning from Linux vocabulary) but the power of a GPU os it can start all threads in one or two instruction and synchronization is done directly on the card, whithout any intervention from the developer.
Example
To use this new concept, the Nvidia add new directive or keywords in the C++ syntax. To use them you must use the Nvidia compiler nvcc.
- CUDA C keyword __global__ indicates that a function runs on the device called from host code (value by default to execute a kernel on a GPU)
- CUDA C keyword __device__ indicates that a function runs on the device called from a device code
- CUDA C keyword __host__ indicates that a function runs on the host (the main CPU)
After all theses consideration, let’s start with a small example.
#include "performancetiming.hpp" #include#include // function to add the elements of two arrays void add(int n, float *x, float *y) { for (int i = 0; i < n; i++) y[i] = x[i] + y[i]; } int main(void) { int N = 1<<24; // 16M elements float *x = new float[N]; float *y = new float[N]; // initialize x and y arrays on the host for (int i = 0; i < N; i++) { x[i] = 1.0f; y[i] = 2.0f; } // Run kernel on 16M elements on the CPU add(N, x, y); float maxError = 0.0f; for (int i = 0; i < N; i++) maxError = fmax(maxError, fabs(y[i]-3.0f)); std::cout << "Max error: " << maxError << std::endl; // Free memory delete [] x; delete [] y; return 0; }
This code is adding number one by one all elements of two arrays and store it in the second. The main processing part is done in add function. Each result is independent so we can