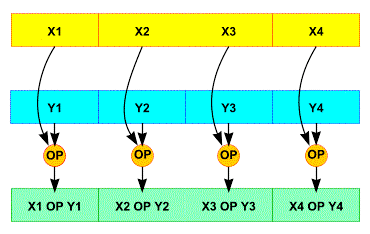
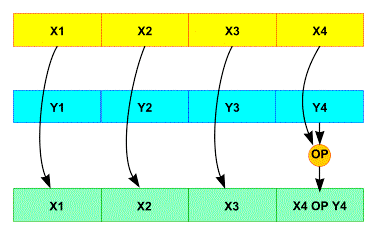
In the previous article we started sha* functions optimizations, now as we previously seen a large bottleneck performance is in internal.c.
/*
This file is part of ethash.
ethash is free software: you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation, either version 3 of the License, or
(at your option) any later version.
ethash is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
GNU General Public License for more details.
You should have received a copy of the GNU General Public License
along with cpp-ethereum. If not, see <http://www.gnu.org/licenses/>.
*/
/** @file internal.c
* @author Tim Hughes <tim@twistedfury.com>
* @author Matthew Wampler-Doty
* @date 2015
*/
#include <assert.h>
#include <inttypes.h>
#include <stddef.h>
#include <errno.h>
#include <math.h>
#include "mmap.h"
#include "ethash.h"
#include "fnv.h"
#include "endian.h"
#include "internal.h"
#include "data_sizes.h"
#include "io.h"
#ifdef WITH_CRYPTOPP
#include "sha3_cryptopp.h"
#else
#include "sha3.h"
#endif // WITH_CRYPTOPP
uint64_t ethash_get_datasize(uint64_t const block_number)
{
assert(block_number / ETHASH_EPOCH_LENGTH < 2048);
return dag_sizes[block_number / ETHASH_EPOCH_LENGTH];
}
uint64_t ethash_get_cachesize(uint64_t const block_number)
{
assert(block_number / ETHASH_EPOCH_LENGTH < 2048);
return cache_sizes[block_number / ETHASH_EPOCH_LENGTH];
}
// Follows Sergio's "STRICT MEMORY HARD HASHING FUNCTIONS" (2014)
// https://bitslog.files.wordpress.com/2013/12/memohash-v0-3.pdf
// SeqMemoHash(s, R, N)
static bool ethash_compute_cache_nodes(
node* const nodes,
uint64_t cache_size,
ethash_h256_t const* seed
)
{
if (cache_size % sizeof(node) != 0) {
return false;
}
uint32_t const num_nodes = (uint32_t) (cache_size / sizeof(node));
SHA3_512(nodes[0].bytes, (uint8_t*)seed, 32);
for (uint32_t i = 1; i != num_nodes; ++i) {
SHA3_512(nodes[i].bytes, nodes[i - 1].bytes, 64);
}
for (uint32_t j = 0; j != ETHASH_CACHE_ROUNDS; j++) {
for (uint32_t i = 0; i != num_nodes; i++) {
uint32_t const idx = nodes[i].words[0] % num_nodes;
node data;
data = nodes[(num_nodes - 1 + i) % num_nodes];
for (uint32_t w = 0; w != NODE_WORDS; ++w) {
data.words[w] ^= nodes[idx].words[w];
}
SHA3_512(nodes[i].bytes, data.bytes, sizeof(data));
}
}
// now perform endian conversion
fix_endian_arr32(nodes->words, num_nodes * NODE_WORDS);
return true;
}
void ethash_calculate_dag_item(
node* const ret,
uint32_t node_index,
ethash_light_t const light
)
{
uint32_t num_parent_nodes = (uint32_t) (light->cache_size / sizeof(node));
node const* cache_nodes = (node const *) light->cache;
node const* init = &cache_nodes[node_index % num_parent_nodes];
memcpy(ret, init, sizeof(node));
ret->words[0] ^= node_index;
SHA3_512(ret->bytes, ret->bytes, sizeof(node));
#if defined(_M_X64) && ENABLE_SSE
__m128i const fnv_prime = _mm_set1_epi32(FNV_PRIME);
__m128i xmm0 = ret->xmm[0];
__m128i xmm1 = ret->xmm[1];
__m128i xmm2 = ret->xmm[2];
__m128i xmm3 = ret->xmm[3];
#elif defined(__MIC__)
__m512i const fnv_prime = _mm512_set1_epi32(FNV_PRIME);
__m512i zmm0 = ret->zmm[0];
#endif
for (uint32_t i = 0; i != ETHASH_DATASET_PARENTS; ++i) {
uint32_t parent_index = fnv_hash(node_index ^ i, ret->words[i % NODE_WORDS]) % num_parent_nodes;
node const *parent = &cache_nodes[parent_index];
#if defined(_M_X64) && ENABLE_SSE
{
xmm0 = _mm_mullo_epi32(xmm0, fnv_prime);
xmm1 = _mm_mullo_epi32(xmm1, fnv_prime);
xmm2 = _mm_mullo_epi32(xmm2, fnv_prime);
xmm3 = _mm_mullo_epi32(xmm3, fnv_prime);
xmm0 = _mm_xor_si128(xmm0, parent->xmm[0]);
xmm1 = _mm_xor_si128(xmm1, parent->xmm[1]);
xmm2 = _mm_xor_si128(xmm2, parent->xmm[2]);
xmm3 = _mm_xor_si128(xmm3, parent->xmm[3]);
// have to write to ret as values are used to compute index
ret->xmm[0] = xmm0;
ret->xmm[1] = xmm1;
ret->xmm[2] = xmm2;
ret->xmm[3] = xmm3;
}
#elif defined(__MIC__)
{
zmm0 = _mm512_mullo_epi32(zmm0, fnv_prime);
// have to write to ret as values are used to compute index
zmm0 = _mm512_xor_si512(zmm0, parent->zmm[0]);
ret->zmm[0] = zmm0;
}
#else
{
for (unsigned w = 0; w != NODE_WORDS; ++w) {
ret->words[w] = fnv_hash(ret->words[w], parent->words[w]);
}
}
#endif
}
SHA3_512(ret->bytes, ret->bytes, sizeof(node));
}
bool ethash_compute_full_data(
void* mem,
uint64_t full_size,
ethash_light_t const light,
ethash_callback_t callback
)
{
if (full_size % (sizeof(uint32_t) * MIX_WORDS) != 0 ||
(full_size % sizeof(node)) != 0) {
return false;
}
uint32_t const max_n = (uint32_t)(full_size / sizeof(node));
node* full_nodes = mem;
double const progress_change = 1.0f / max_n;
double progress = 0.0f;
// now compute full nodes
for (uint32_t n = 0; n != max_n; ++n) {
if (callback &&
n % (max_n / 100) == 0 &&
callback((unsigned int)(ceil(progress * 100.0f))) != 0) {
return false;
}
progress += progress_change;
ethash_calculate_dag_item(&(full_nodes[n]), n, light);
}
return true;
}
static bool ethash_hash(
ethash_return_value_t* ret,
node const* full_nodes,
ethash_light_t const light,
uint64_t full_size,
ethash_h256_t const header_hash,
uint64_t const nonce
)
{
if (full_size % MIX_WORDS != 0) {
return false;
}
// pack hash and nonce together into first 40 bytes of s_mix
assert(sizeof(node) * 8 == 512);
node s_mix[MIX_NODES + 1];
memcpy(s_mix[0].bytes, &header_hash, 32);
fix_endian64(s_mix[0].double_words[4], nonce);
// compute sha3-512 hash and replicate across mix
SHA3_512(s_mix->bytes, s_mix->bytes, 40);
fix_endian_arr32(s_mix[0].words, 16);
node* const mix = s_mix + 1;
for (uint32_t w = 0; w != MIX_WORDS; ++w) {
mix->words[w] = s_mix[0].words[w % NODE_WORDS];
}
unsigned const page_size = sizeof(uint32_t) * MIX_WORDS;
unsigned const num_full_pages = (unsigned) (full_size / page_size);
for (unsigned i = 0; i != ETHASH_ACCESSES; ++i) {
uint32_t const index = fnv_hash(s_mix->words[0] ^ i, mix->words[i % MIX_WORDS]) % num_full_pages;
for (unsigned n = 0; n != MIX_NODES; ++n) {
node const* dag_node;
node tmp_node;
if (full_nodes) {
dag_node = &full_nodes[MIX_NODES * index + n];
} else {
ethash_calculate_dag_item(&tmp_node, index * MIX_NODES + n, light);
dag_node = &tmp_node;
}
#if defined(_M_X64) && ENABLE_SSE
{
__m128i fnv_prime = _mm_set1_epi32(FNV_PRIME);
__m128i xmm0 = _mm_mullo_epi32(fnv_prime, mix[n].xmm[0]);
__m128i xmm1 = _mm_mullo_epi32(fnv_prime, mix[n].xmm[1]);
__m128i xmm2 = _mm_mullo_epi32(fnv_prime, mix[n].xmm[2]);
__m128i xmm3 = _mm_mullo_epi32(fnv_prime, mix[n].xmm[3]);
mix[n].xmm[0] = _mm_xor_si128(xmm0, dag_node->xmm[0]);
mix[n].xmm[1] = _mm_xor_si128(xmm1, dag_node->xmm[1]);
mix[n].xmm[2] = _mm_xor_si128(xmm2, dag_node->xmm[2]);
mix[n].xmm[3] = _mm_xor_si128(xmm3, dag_node->xmm[3]);
}
#elif defined(__MIC__)
{
// __m512i implementation via union
// Each vector register (zmm) can store sixteen 32-bit integer numbers
__m512i fnv_prime = _mm512_set1_epi32(FNV_PRIME);
__m512i zmm0 = _mm512_mullo_epi32(fnv_prime, mix[n].zmm[0]);
mix[n].zmm[0] = _mm512_xor_si512(zmm0, dag_node->zmm[0]);
}
#else
{
for (unsigned w = 0; w != NODE_WORDS; ++w) {
mix[n].words[w] = fnv_hash(mix[n].words[w], dag_node->words[w]);
}
}
#endif
}
}
// Workaround for a GCC regression which causes a bogus -Warray-bounds warning.
// The regression was introduced in GCC 4.8.4, fixed in GCC 5.0.0 and backported to GCC 4.9.3 but
// never to the GCC 4.8.x line.
//
// See https://gcc.gnu.org/bugzilla/show_bug.cgi?id=56273
//
// This regression is affecting Debian Jesse (8.5) builds of cpp-ethereum (GCC 4.9.2) and also
// manifests in the doublethinkco armel v5 cross-builds, which use crosstool-ng and resulting
// in the use of GCC 4.8.4. The Tizen runtime wants an even older GLIBC version - the one from
// GCC 4.6.0!
#if defined(__GNUC__) && (__GNUC__ < 5)
#pragma GCC diagnostic push
#pragma GCC diagnostic ignored "-Warray-bounds"
#endif // define (__GNUC__)
// compress mix
for (uint32_t w = 0; w != MIX_WORDS; w += 4) {
uint32_t reduction = mix->words[w + 0];
reduction = reduction * FNV_PRIME ^ mix->words[w + 1];
reduction = reduction * FNV_PRIME ^ mix->words[w + 2];
reduction = reduction * FNV_PRIME ^ mix->words[w + 3];
mix->words[w / 4] = reduction;
}
#if defined(__GNUC__) && (__GNUC__ < 5)
#pragma GCC diagnostic pop
#endif // define (__GNUC__)
fix_endian_arr32(mix->words, MIX_WORDS / 4);
memcpy(&ret->mix_hash, mix->bytes, 32);
// final Keccak hash
SHA3_256(&ret->result, s_mix->bytes, 64 + 32); // Keccak-256(s + compressed_mix)
return true;
}
void ethash_quick_hash(
ethash_h256_t* return_hash,
ethash_h256_t const* header_hash,
uint64_t const nonce,
ethash_h256_t const* mix_hash
)
{
uint8_t buf[64 + 32];
memcpy(buf, header_hash, 32);
fix_endian64_same(nonce);
memcpy(&(buf[32]), &nonce, 8);
SHA3_512(buf, buf, 40);
memcpy(&(buf[64]), mix_hash, 32);
SHA3_256(return_hash, buf, 64 + 32);
}
ethash_h256_t ethash_get_seedhash(uint64_t block_number)
{
ethash_h256_t ret;
ethash_h256_reset(&ret);
uint64_t const epochs = block_number / ETHASH_EPOCH_LENGTH;
for (uint32_t i = 0; i < epochs; ++i)
SHA3_256(&ret, (uint8_t*)&ret, 32);
return ret;
}
bool ethash_quick_check_difficulty(
ethash_h256_t const* header_hash,
uint64_t const nonce,
ethash_h256_t const* mix_hash,
ethash_h256_t const* boundary
)
{
ethash_h256_t return_hash;
ethash_quick_hash(&return_hash, header_hash, nonce, mix_hash);
return ethash_check_difficulty(&return_hash, boundary);
}
ethash_light_t ethash_light_new_internal(uint64_t cache_size, ethash_h256_t const* seed)
{
struct ethash_light *ret;
ret = calloc(sizeof(*ret), 1);
if (!ret) {
return NULL;
}
#if defined(__MIC__)
ret->cache = _mm_malloc((size_t)cache_size, 64);
#else
ret->cache = malloc((size_t)cache_size);
#endif
if (!ret->cache) {
goto fail_free_light;
}
node* nodes = (node*)ret->cache;
if (!ethash_compute_cache_nodes(nodes, cache_size, seed)) {
goto fail_free_cache_mem;
}
ret->cache_size = cache_size;
return ret;
fail_free_cache_mem:
#if defined(__MIC__)
_mm_free(ret->cache);
#else
free(ret->cache);
#endif
fail_free_light:
free(ret);
return NULL;
}
ethash_light_t ethash_light_new(uint64_t block_number)
{
ethash_h256_t seedhash = ethash_get_seedhash(block_number);
ethash_light_t ret;
ret = ethash_light_new_internal(ethash_get_cachesize(block_number), &seedhash);
ret->block_number = block_number;
return ret;
}
void ethash_light_delete(ethash_light_t light)
{
if (light->cache) {
free(light->cache);
}
free(light);
}
ethash_return_value_t ethash_light_compute_internal(
ethash_light_t light,
uint64_t full_size,
ethash_h256_t const header_hash,
uint64_t nonce
)
{
ethash_return_value_t ret;
ret.success = true;
if (!ethash_hash(&ret, NULL, light, full_size, header_hash, nonce)) {
ret.success = false;
}
return ret;
}
ethash_return_value_t ethash_light_compute(
ethash_light_t light,
ethash_h256_t const header_hash,
uint64_t nonce
)
{
uint64_t full_size = ethash_get_datasize(light->block_number);
return ethash_light_compute_internal(light, full_size, header_hash, nonce);
}
static bool ethash_mmap(struct ethash_full* ret, FILE* f)
{
int fd;
char* mmapped_data;
errno = 0;
ret->file = f;
if ((fd = ethash_fileno(ret->file)) == -1) {
return false;
}
mmapped_data = mmap(
NULL,
(size_t)ret->file_size + ETHASH_DAG_MAGIC_NUM_SIZE,
PROT_READ | PROT_WRITE,
MAP_SHARED,
fd,
0
);
if (mmapped_data == MAP_FAILED) {
return false;
}
ret->data = (node*)(mmapped_data + ETHASH_DAG_MAGIC_NUM_SIZE);
return true;
}
ethash_full_t ethash_full_new_internal(
char const* dirname,
ethash_h256_t const seed_hash,
uint64_t full_size,
ethash_light_t const light,
ethash_callback_t callback
)
{
struct ethash_full* ret;
FILE *f = NULL;
ret = calloc(sizeof(*ret), 1);
if (!ret) {
return NULL;
}
ret->file_size = (size_t)full_size;
enum ethash_io_rc err = ethash_io_prepare(dirname, seed_hash, &f, (size_t)full_size, false);
if (err == ETHASH_IO_FAIL)
goto fail_free_full;
if (err == ETHASH_IO_MEMO_SIZE_MISMATCH) {
// if a DAG of same filename but unexpected size is found, silently force new file creation
if (ethash_io_prepare(dirname, seed_hash, &f, (size_t)full_size, true) != ETHASH_IO_MEMO_MISMATCH) {
ETHASH_CRITICAL("Could not recreate DAG file after finding existing DAG with unexpected size.");
goto fail_free_full;
}
// we now need to go through the mismatch case, NOT the match case
err = ETHASH_IO_MEMO_MISMATCH;
}
if (err == ETHASH_IO_MEMO_MISMATCH || err == ETHASH_IO_MEMO_MATCH) {
if (!ethash_mmap(ret, f)) {
ETHASH_CRITICAL("mmap failure()");
goto fail_close_file;
}
if (err == ETHASH_IO_MEMO_MATCH) {
#if defined(__MIC__)
node* tmp_nodes = _mm_malloc((size_t)full_size, 64);
//copy all nodes from ret->data
//mmapped_nodes are not aligned properly
uint32_t const countnodes = (uint32_t) ((size_t)ret->file_size / sizeof(node));
//fprintf(stderr,"ethash_full_new_internal:countnodes:%d",countnodes);
for (uint32_t i = 1; i != countnodes; ++i) {
tmp_nodes[i] = ret->data[i];
}
ret->data = tmp_nodes;
#endif
return ret;
}
}
#if defined(__MIC__)
ret->data = _mm_malloc((size_t)full_size, 64);
#endif
if (!ethash_compute_full_data(ret->data, full_size, light, callback)) {
ETHASH_CRITICAL("Failure at computing DAG data.");
goto fail_free_full_data;
}
// after the DAG has been filled then we finalize it by writting the magic number at the beginning
if (fseek(f, 0, SEEK_SET) != 0) {
ETHASH_CRITICAL("Could not seek to DAG file start to write magic number.");
goto fail_free_full_data;
}
uint64_t const magic_num = ETHASH_DAG_MAGIC_NUM;
if (fwrite(&magic_num, ETHASH_DAG_MAGIC_NUM_SIZE, 1, f) != 1) {
ETHASH_CRITICAL("Could not write magic number to DAG's beginning.");
goto fail_free_full_data;
}
if (fflush(f) != 0) {// make sure the magic number IS there
ETHASH_CRITICAL("Could not flush memory mapped data to DAG file. Insufficient space?");
goto fail_free_full_data;
}
return ret;
fail_free_full_data:
// could check that munmap(..) == 0 but even if it did not can't really do anything here
munmap(ret->data, (size_t)full_size);
#if defined(__MIC__)
_mm_free(ret->data);
#endif
fail_close_file:
fclose(ret->file);
fail_free_full:
free(ret);
return NULL;
}
ethash_full_t ethash_full_new(ethash_light_t light, ethash_callback_t callback)
{
char strbuf[256];
if (!ethash_get_default_dirname(strbuf, 256)) {
return NULL;
}
uint64_t full_size = ethash_get_datasize(light->block_number);
ethash_h256_t seedhash = ethash_get_seedhash(light->block_number);
return ethash_full_new_internal(strbuf, seedhash, full_size, light, callback);
}
void ethash_full_delete(ethash_full_t full)
{
// could check that munmap(..) == 0 but even if it did not can't really do anything here
munmap(full->data, (size_t)full->file_size);
if (full->file) {
fclose(full->file);
}
free(full);
}
ethash_return_value_t ethash_full_compute(
ethash_full_t full,
ethash_h256_t const header_hash,
uint64_t nonce
)
{
ethash_return_value_t ret;
ret.success = true;
if (!ethash_hash(
&ret,
(node const*)full->data,
NULL,
full->file_size,
header_hash,
nonce)) {
ret.success = false;
}
return ret;
}
void const* ethash_full_dag(ethash_full_t full)
{
return full->data;
}
uint64_t ethash_full_dag_size(ethash_full_t full)
{
return full->file_size;
}
The code is now a bit complex comparing to sha_256 functions, functions are longer and they interleave assembler directive.
Remove unecessay tests et precalculated all data
Remember that a test reinitialize the pipeline of the processor because it implies a jump instruction and as a result kills the sequence of instruction. So if we use “constant” or well known values we can drop tests guard test at the start of function. Note it is not necessary to remove assert function. Indeed theses functions are only generated on debug mode, so a good practice is to use assert as replacement of if to test parameters values.
We can also specialize function (see previous post for example) to remove constant parameters. The aim is to create sha_256_32 when size is 32, sha_256_64 when size is 64 and keep a generic function with a parameter when we can not decide what the size is. The counterpart of this method is it increasing the code size, and we have three duplicate code. So the maintenance will be harder. We can do the same with ethash_hash to remove full_nodes parameter and then remove the test of full_nodes != null line 222.
for (unsigned n = 0; n != MIX_NODES; ++n) { node const* dag_node; node tmp_node; ethash_calculate_dag_item(&tmp_node, index * MIX_NODES + n, light); …. } can be changed to
unsigned preindex = MIX_NODES * index ;
for (unsigned n = 0; n != MIX_NODES; ++n) {
node const* dag_node;
dag_node = &full_nodes[preindex++];
The differnce is slighty but we replace a leal (load effective adress, which access to register, this code is called 64 times so we saved a little bit of time.

Let’s doing a performance test:
./eth -M -t 1 --benchmark-trial 15
cpp-ethereum, a C++ Ethereum client
04:43:41 PM.112|eth #00004000…
Benchmarking on platform: 8-thread CPU
Preparing DAG...
Warming up...
04:43:41 PM.112|miner0 Loading full DAG of seedhash: #00000000…
04:43:42 PM.008|miner0 Full DAG loaded
Trial 1... 99273
Trial 2... 101280
Trial 3... 102040
Trial 4... 100733
Trial 5... 101026
min/mean/max: 99273/100870/102040 H/s
inner mean: 101013 H/s
Not bad result, it is the first time we exced 100k H/s.
If you want to test you can get the V1.2 tag,
Specific optimization
Right now the code is written in “pure” C, it means that this code can be without too much effort compiled from raspberry to last end Intel processor.
The last step of optimization is now specific to the target. In this phase we will optimize the code for a specific platform, in our example we will use 128 bits register included in SSE2.0, as a counterpart the code will only work on 64 bits Intel/Amd processor.
In this project implementation had been already done with SSE registers but this cannot be able. In fact to enable this generation you have to done two things:
- Tell the compiler that you want to use SSE instructions
- Set ENABLE_SSE define to true line 7 in internal.h file
The question you might ask, why this option is not always set to true, and why every modern processor do not use SSE instructions by default ? The answer is not only for historical reasons, but also for performance reason which is at first sight seems contra-intuitive. Indeed if we enable SSE we have more register for us, but switching task will be longer because the processor has to save more registers, and theses registers are essentially used for intensive calculus and are useless on common computer tasks.