People often ask me what is the best way to optimize code and cope which is the best way to optimize code. The best way to understand how to do that is to take an example. I’m gonna show you how to optimize the implementation of the ethereum algorithm. This miner has also a very useful command to determine the hashrate. It will help us to know the performance improvement. To help you to follow the process I added tag for the differents steps exposed below.
git clone --recursive https://github.com/fflayol/cpp-ethereum.git cd cpp-ethereum mkdir build cd build cmake ..; make -j3 cd eth make ./eth -M -t 1 --benchmark-trial 15
It gives
~/Perso/mod/cpp-ethereum/build/eth$ ./eth -M -t 1 --benchmark-trial 15
cpp-ethereum, a C++ Ethereum client
03:11:20 PM.445|eth #00004000…
Benchmarking on platform: 8-thread CPU
Preparing DAG...
Warming up...
03:11:20 PM.445|miner0 Loading full DAG of seedhash: #00000000…
03:11:21 PM.438|miner0 Full DAG loaded
Trial 1... 86326
Trial 2... 90166
Trial 3... 91300
Trial 4... 97646
Trial 5... 95880
min/mean/max: 86326/92263/97646 H/s
inner mean: 92448 H/s
The last command give us a reference of performance to see our improvement.
What to optimize
To start optimization we have to know which function last the more. For this purpose we can use valgrind (callgrind).
valgrind --tool=callgrind ./eth -M -t 1 --benchmark-trial 15
After execution callgrind save a file that you can read with kcachegrind.
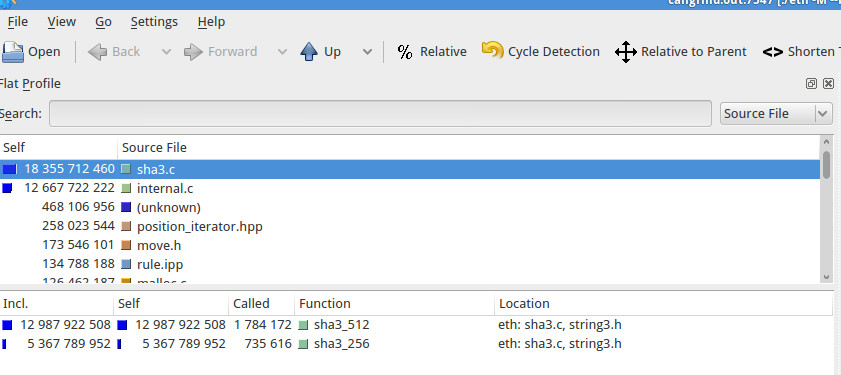
If we order by execution time, two files are very time consuming .If we focus on sha3.c two functions are very time consuming sha3_512 and sha3_256. If we optimize a bit theses two functions the program itself will be faster. I will now show you different step used to optimize as fast as possible.
Be careful when you use this kind of optimization has several dropdown:
- Code will become hardly to maintain and to understand. So do theses optimizations on well testing and covered code.
- To maximize gain you have to be as close as possible on the target so porting optimization from a target to another should be very difficult.
Ensure that call to functions are optimal
Let’s start with sha3.c file
/** libkeccak-tiny
*
* A single-file implementation of SHA-3 and SHAKE.
*
* Implementor: David Leon Gil
* License: CC0, attribution kindly requested. Blame taken too,
* but not liability.
*/
#include "sha3.h"
#include <stdint.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
/******** The Keccak-f[1600] permutation ********/
/*** Constants. ***/
static const uint8_t rho[24] = \
{ 1, 3, 6, 10, 15, 21,
28, 36, 45, 55, 2, 14,
27, 41, 56, 8, 25, 43,
62, 18, 39, 61, 20, 44};
static const uint8_t pi[24] = \
{10, 7, 11, 17, 18, 3,
5, 16, 8, 21, 24, 4,
15, 23, 19, 13, 12, 2,
20, 14, 22, 9, 6, 1};
static const uint64_t RC[24] = \
{1ULL, 0x8082ULL, 0x800000000000808aULL, 0x8000000080008000ULL,
0x808bULL, 0x80000001ULL, 0x8000000080008081ULL, 0x8000000000008009ULL,
0x8aULL, 0x88ULL, 0x80008009ULL, 0x8000000aULL,
0x8000808bULL, 0x800000000000008bULL, 0x8000000000008089ULL, 0x8000000000008003ULL,
0x8000000000008002ULL, 0x8000000000000080ULL, 0x800aULL, 0x800000008000000aULL,
0x8000000080008081ULL, 0x8000000000008080ULL, 0x80000001ULL, 0x8000000080008008ULL};
/*** Helper macros to unroll the permutation. ***/
#define rol(x, s) (((x) << s) | ((x) >> (64 - s)))
#define REPEAT6(e) e e e e e e
#define REPEAT24(e) REPEAT6(e e e e)
#define REPEAT5(e) e e e e e
#define FOR5(v, s, e) \
v = 0; \
REPEAT5(e; v += s;)
/*** Keccak-f[1600] ***/
static inline void keccakf(void* state) {
uint64_t* a = (uint64_t*)state;
uint64_t b[5] = {0};
uint64_t t = 0;
uint8_t x, y;
for (int i = 0; i < 24; i++) {
// Theta
FOR5(x, 1,
b[x] = 0;
FOR5(y, 5,
b[x] ^= a[x + y]; ))
FOR5(x, 1,
FOR5(y, 5,
a[y + x] ^= b[(x + 4) % 5] ^ rol(b[(x + 1) % 5], 1); ))
// Rho and pi
t = a[1];
x = 0;
REPEAT24(b[0] = a[pi[x]];
a[pi[x]] = rol(t, rho[x]);
t = b[0];
x++; )
// Chi
FOR5(y,
5,
FOR5(x, 1,
b[x] = a[y + x];)
FOR5(x, 1,
a[y + x] = b[x] ^ ((~b[(x + 1) % 5]) & b[(x + 2) % 5]); ))
// Iota
a[0] ^= RC[i];
}
}
/******** The FIPS202-defined functions. ********/
/*** Some helper macros. ***/
#define _(S) do { S } while (0)
#define FOR(i, ST, L, S) \
_(for (size_t i = 0; i < L; i += ST) { S; })
#define mkapply_ds(NAME, S) \
static inline void NAME(uint8_t* dst, \
const uint8_t* src, \
size_t len) { \
FOR(i, 1, len, S); \
}
#define mkapply_sd(NAME, S) \
static inline void NAME(const uint8_t* src, \
uint8_t* dst, \
size_t len) { \
FOR(i, 1, len, S); \
}
mkapply_ds(xorin, dst[i] ^= src[i]) // xorin
mkapply_sd(setout, dst[i] = src[i]) // setout
#define P keccakf
#define Plen 200
// Fold P*F over the full blocks of an input.
#define foldP(I, L, F) \
while (L >= rate) { \
F(a, I, rate); \
P(a); \
I += rate; \
L -= rate; \
}
/** The sponge-based hash construction. **/
static inline int hash(uint8_t* out, size_t outlen,
const uint8_t* in, size_t inlen,
size_t rate, uint8_t delim) {
if ((out == NULL) || ((in == NULL) && inlen != 0) || (rate >= Plen)) {
return -1;
}
uint8_t a[Plen] = {0};
// Absorb input.
foldP(in, inlen, xorin);
// Xor in the DS and pad frame.
a[inlen] ^= delim;
a[rate - 1] ^= 0x80;
// Xor in the last block.
xorin(a, in, inlen);
// Apply P
P(a);
// Squeeze output.
foldP(out, outlen, setout);
setout(a, out, outlen);
memset(a, 0, 200);
return 0;
}
#define defsha3(bits) \
int sha3_##bits(uint8_t* out, size_t outlen, \
const uint8_t* in, size_t inlen) { \
if (outlen > (bits/8)) { \
return -1; \
} \
return hash(out, outlen, in, inlen, 200 - (bits / 4), 0x01); \
}
/*** FIPS202 SHA3 FOFs ***/
defsha3(256)
defsha3(512)
defsha3_256 et defsha3_512 are macro function with a parameter, so the first step here is to “specialize them” in function and the inline them. So the code becomes the following:
inline int sha3_256(uint8_t* out, size_t outlen, const uint8_t* in, size_t inlen)
{
if (outlen > 32)
{
return -1;
}
return hash(out, outlen, in, inlen, 136, 0x01);
}
inline int sha3_512(uint8_t* out, size_t outlen, const uint8_t* in, size_t inlen)
{
if (outlen > 64)
{
return -1;
}
return hash(out, outlen, in, inlen, 72, 0x01);
}
The performance results will be strictly the same , so what is the aim of this optimization ? It shows that sha3_256 and sha3_512 are wrappers to hash function.
This hash function is static, so only called in this file and what is interesting here is that this function is called with one parameter set to 0x01 and another with only two differents values.
So int he first step we can remove delim parameter in hash function. Why is it important ? If we use constant functions the compiler will easily optimize our code by pre-calculating values, allocation and removing tests.
For instance:
int foo(int size){
if (size == 0){
return 0;
}
return size +1;
}
main(){
cout<< foo (10)<<endl;
}
In the code upper the test (size ==0) is totally useless, so the compiler can remove the call to foo and replacing it with 11.
Now for our hash function we can remove the delim parameter and the test for rate value, which gives:
/** The sponge-based hash construction. **/
static inline int hash(
uint8_t* out, size_t outlen, const uint8_t* in, size_t inlen, size_t rate)
{
if ((out == NULL) || ((in == NULL) && inlen != 0))
{
return -1;
}
uint8_t a[Plen] = {0};
// Absorb input.
foldP(in, inlen, xorin);
// Xor in the DS and pad frame.
a[inlen] ^= 0x01;
a[rate - 1] ^= 0x80;
// Xor in the last block.
xorin(a, in, inlen);
// Apply P
P(a);
// Squeeze output.
foldP(out, outlen, setout);
setout(a, out, outlen);
memset(a, 0, 200);
return 0;
}
inline int sha3_256(uint8_t* out, size_t outlen, const uint8_t* in, size_t inlen)
{
if (outlen > 32)
{
return -1;
}
return hash(out, outlen, in, inlen, 136);
}
inline int sha3_512(uint8_t* out, size_t outlen, const uint8_t* in, size_t inlen)
{
if (outlen > 64)
{
return -1;
}
return hash(out, outlen, in, inlen, 72);
}
Surprisingly it is still possible to optimize sha3_512 and sha3_256. If you do a search to know where theses functions are used you’ll find that 256 is always called with outlen set to 32 and for sha3_512 outlen is set to 64. So we can remove this parameter in both functions.
static inline int hash(
uint8_t* out, size_t outlen, const uint8_t* in, size_t inlen, size_t rate)
{
if ((out == NULL) || ((in == NULL) && inlen != 0) )
{
return -1;
}
uint8_t a[Plen] = {0};
// Absorb input.
foldP(in, inlen, xorin);
// Xor in the DS and pad frame.
a[inlen] ^= 0x01;
a[rate - 1] ^= 0x80;
// Xor in the last block.
xorin(a, in, inlen);
// Apply P
P(a);
// Squeeze output.
foldP(out, outlen, setout);
setout(a, out, outlen);
memset(a, 0, 200);
return 0;
}
inline int sha3_256(uint8_t* out, const uint8_t* in, size_t inlen)
{
return hash(out, 32, in, inlen, 136);
}
inline int sha3_512(uint8_t* out, const uint8_t* in, size_t inlen)
{
return hash(out, 64, in, inlen, 72);
}
You have also to change sha3.h. We’ve arrived to a milestone, I added a tag in git for this first part. To get the version
git checkout V1.1
Now it is time to see the results:
~/Perso/mod/cpp-ethereum/build/eth$ ./eth -M -t 1 --benchmark-trial 15
cpp-ethereum, a C++ Ethereum client
03:02:13 PM.558|eth #00004000…
Benchmarking on platform: 8-thread CPU
Preparing DAG...
Warming up...
03:02:13 PM.558|miner0 Loading full DAG of seedhash: #00000000…
03:02:14 PM.476|miner0 Full DAG loaded
Trial 1... 98380
Trial 2... 98653
Trial 3... 96666
Trial 4... 97993
Trial 5... 97900
min/mean/max: 96666/97918/98653 H/s
inner mean: 98091 H/s
The results are quite good (98091 vs 92448 106 percent faster). Honestly as we do not use the same input I think that the increasing is more like 104%.
So why by modifying and simplifying calls to function we have a such gain ? The reason is that modern processors do not like functions calls, they get their best performance when instructions are sequential. It allows the processor to re-arrange instructions and execute several in parallel.
Validation
After all theses modifications you must launch tests to ensure you didn’t broke anything. If the tests cover a good part of the code, it will guarantee you that your modifications didn’t break anything.
cd build make test
Conclusion
We showed that with two hours of work,even on latest compiler optimization there’s still a way to optimize code without too much effort and in this case without compromising the readability of the code. In the next post it won’t be the case 🙂